本文共 2867 字，大约阅读时间需要 9 分钟。

1、题目描述

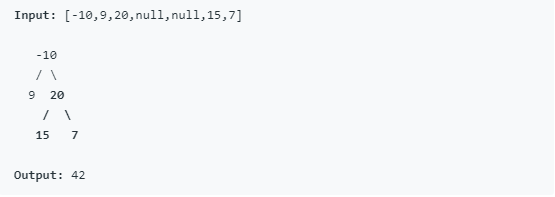
    输入一棵二叉树，求这课二叉树所有路径中最大的路径和。比如输入二叉树为：[-10,9,20,null,null,15,7]，输出：42。

2、解题思路

    我们知道，给定一个数组，求这个数组的连续子数组的最大和是比较容易的。而这道题目是将二叉树与连续子数组的最大和糅合在一起。因此我们需要在递归中求出二叉树路径的连续子数组的最大和。因此，在二叉树的递归函数中，输入一个节点，我们需要求出以这个节点为根的二叉树的连续子数组的最大和。递归函数进行如下判断：

• 如果节点的左子树和右子树为空，那么连续子数组的最大和为这个节点值。
• 如果左子树不为空，那么遍历左子树，求出以左子树为根的树中连续子数组的最大和。
• 如果右子树不为空，那么遍历右子树，求出以右子树为根的树中连续子数组的最大和。
• 接着对从左子树最大和、右子树最大和、节点值、左子树最大和 + 节点值、右子树最大和 + 节点值、左子树+右子树+节点值中取出最大的保存即可。

    int maxPathSum(TreeNode* root) {        if(root==nullptr)            return 0;        int sum = 0;        int max_len = root->val;        max_path(root,max_len,sum);        return max_len;    }    void max_path(TreeNode *p,int &max_len,int &sum){        int left = 0;                               //左子树的路径最大路径和        int right = 0;                              //右子树路径的最大路径和        int left_sum=0;                             //左子树加上根节点的最大路径和        int right_sum=0;                            //右子树加上根节点的最大路径和        if(p->left==nullptr&&p->right==nullptr){    //左右子树都为空，路劲和为节点值            sum = p->val;            max_len = max_len > p->val ? max_len : p->val;            return;        }        if(p->left&&p->right){                     //左右子树都不为空，则分开求            max_path(p->left,max_len,left);            max_path(p->right,max_len,right);            if(left < 0)                left_sum = p->val;            else                left_sum = left + p->val;            if(right < 0)                right_sum = p->val;            else                right_sum = right + p->val;            sum = left_sum > right_sum?left_sum:right_sum;            max_len = Max2(max_len,left,right,left + right + p->val,p->val,sum);            return;        }        if(p->left==nullptr&&p->right){            //左子树为空，右子树不为空            max_path(p->right,max_len,right);            if(right < 0)                right_sum = p->val;            else                right_sum = right + p->val;            sum = right_sum;             max_len = Max(right,max_len,p->val,right + p->val,right_sum);            return;        }        if(p->right==nullptr&&p->left){          //右子树为空，左子树不为空            max_path(p->left,max_len,left);            if(left < 0)                left_sum = p->val;            else                left_sum = left + p->val;            sum = left_sum;            max_len = Max(left, max_len ,p->val,left + p->val,sum);            return;        }                        }    int Max(int a,int b,int c,int d,int e){         //求5个数的最大值        int temp = a;        if(temp<b) temp = b;        if(temp<c) temp = c;        if(temp<d) temp = d;        if(temp<e) temp = e;        return temp;    }    int Max2(int a,int b,int c,int d,int e,int f){  //求6个数的最大值        int temp = a;        if(temp<b) temp = b;        if(temp<c) temp = c;        if(temp<d) temp = d;        if(temp<e) temp = e;        if(temp<f) temp = f;        return temp;            }

转载地址：http://zdqe.baihongyu.com/